on
Blog 5: The Air War - Advertisements
Introduction
This week, I explored the effect of political advertisements on the Democratic vote share at the Congressional district level. Using political advertisement data from 2006-2018, I am able to run models for 152 congressional districts. Then, I specifically looked at Pennsylvania’s 10th district to make a model that includes both Democratic advertisement share (%) and Democratic generic ballot polling and to make a prediction for this district’s Democratic vote share in 2022.
In the United States, it’s not election season without a bombardment of political ads. According to a CNBC article from September 2022, campaigns in the 2022 elections have poured $6.4 billion into TV, radio and digital ads for U.S. House, Senate, gubernatorial and local races. The 2022 election is on track to become the most expensive election ever. But do these ads actually change voters’ opinions or are they just a waste of money?
Prior Literature
Gerber and authors ran an experiment on the effects of TV and radio advertising on voting preferences. The authors found a “rapid decay of advertising effects” in which “televised ads have strong but short-lived effects on voting preferences” (Gerber et al., 2011). This matches with the exploration we did in section where we found that both Democrats and Republicans spend the most on TV ads closest to the election.
Do Ads Matter in 152 Congressional Districts from 2006-2018?
With this theoretical background, I now explore the relationship between Democratic advertisement share (the percentage of ads run in the district that were for the Democratic candidate) and Democratic vote share in 152 congressional districts from 2006-2018. My main data set that I will be using is from the Wesleyan Media Project, which tracks political TV advertisements.
I ran a simple linear regression model between Democratic vote share and Democratic ad share for 152 congressional districts. The table below shows each district’s linear regression model and its r-squared value and coefficient for Democratic ad share. To interpret the coefficient, it is for every 1% increase in Democratic ad share, there is X% increase/decrease in Democratic vote share.
## # A tibble: 152 × 4
## state st_cd_fips r_squared coefficient
## <chr> <chr> <dbl> <dbl>
## 1 Alabama 0102 1 0.276
## 2 Alabama 0106 0.995 -0.124
## 3 Arizona 0401 0.738 0.153
## 4 Arizona 0402 1.00 0.270
## 5 Arizona 0405 1 -0.561
## 6 Arizona 0408 0.666 1.69
## 7 Arizona 0409 1 0.173
## 8 Arkansas 0501 1 0.163
## 9 Arkansas 0502 0.120 0.180
## 10 Arkansas 0504 0.742 0.225
## 11 California 0603 1 -0.565
## 12 California 0607 1.00 0.158
## 13 California 0610 1 51.0
## 14 California 0611 1 -0.0857
## 15 California 0616 1 0.0268
## 16 California 0620 1 -0.920
## 17 California 0621 0.895 0.0880
## 18 California 0624 0.754 -0.0506
## 19 California 0636 0.661 0.191
## 20 California 0652 0.933 0.387
## 21 Colorado 0803 0.992 0.559
## 22 Colorado 0804 1 -0.360
## 23 Colorado 0806 0.0539 0.423
## 24 Colorado 0807 0.358 -0.0178
## 25 Connecticut 0902 1 0.227
## 26 Connecticut 0904 1 3.34
## 27 Connecticut 0905 0.258 -0.0710
## 28 Florida 1202 0.787 -0.291
## 29 Florida 1208 1 -0.243
## 30 Florida 1209 1 0.467
## 31 Florida 1213 0.00932 0.0808
## 32 Florida 1216 1 0.283
## 33 Florida 1218 0.738 0.269
## 34 Florida 1219 0.488 0.238
## 35 Florida 1222 0.315 0.278
## 36 Florida 1226 0.562 -0.263
## 37 Georgia 1302 1 -19.4
## 38 Georgia 1312 0.291 0.188
## 39 Hawaii 1501 0.618 -0.107
## 40 Idaho 1601 0.161 -0.177
## 41 Idaho 1602 1 0.0810
## 42 Illinois 1708 1 0.0500
## 43 Illinois 1710 0.0000389 0.00106
## 44 Illinois 1711 1 -0.336
## 45 Illinois 1712 0.173 -0.415
## 46 Illinois 1713 1 -2.37
## 47 Illinois 1717 0.0823 0.0831
## 48 Indiana 1802 0.663 0.736
## 49 Indiana 1803 1 0.333
## 50 Indiana 1807 1 -0.191
## 51 Indiana 1808 0.892 0.926
## 52 Indiana 1809 0.0245 0.0330
## 53 Iowa 1901 0.555 -0.626
## 54 Iowa 1902 0.558 0.177
## 55 Iowa 1903 0.00114 -0.0140
## 56 Iowa 1904 0.325 -0.0791
## 57 Kansas 2001 1 -0.0500
## 58 Kansas 2003 0.983 0.331
## 59 Kansas 2004 1 0.281
## 60 Kentucky 2103 0.300 0.400
## 61 Kentucky 2106 0.887 0.312
## 62 Louisiana 2203 0.663 0.628
## 63 Louisiana 2204 0.274 -0.111
## 64 Maine 2301 0.186 -0.0455
## 65 Maine 2302 0.964 1.16
## 66 Maryland 2402 1 0.128
## 67 Massachusetts 2504 1 0.282
## 68 Massachusetts 2506 0.590 0.110
## 69 Michigan 2606 0.309 -0.0849
## 70 Michigan 2607 0.999 -0.122
## 71 Michigan 2608 1 0.125
## 72 Michigan 2611 0.954 0.238
## 73 Minnesota 2702 0.944 0.127
## 74 Minnesota 2703 1 0.0225
## 75 Minnesota 2706 0.977 -0.611
## 76 Minnesota 2707 1 0.372
## 77 Minnesota 2708 0.137 0.141
## 78 Mississippi 2802 1 -2.20
## 79 Missouri 2904 1 0.521
## 80 Missouri 2908 0.0556 -0.0198
## 81 Nebraska 3102 0.570 0.394
## 82 Nevada 3203 0.870 0.317
## 83 Nevada 3204 0.918 -0.231
## 84 New Hampshire 3301 0.864 0.299
## 85 New Hampshire 3302 0.0227 0.0205
## 86 New Jersey 3403 0.781 0.0544
## 87 New Mexico 3501 0.986 0.190
## 88 New Mexico 3502 0.629 0.531
## 89 New York 3601 0.363 -0.117
## 90 New York 3603 1 0.303
## 91 New York 3618 1 0.0240
## 92 New York 3619 0.105 0.287
## 93 New York 3620 0.526 0.399
## 94 New York 3621 0.211 -0.720
## 95 New York 3622 1 0.154
## 96 New York 3623 0.225 -0.200
## 97 New York 3624 0.547 -0.734
## 98 New York 3625 0.0491 0.0528
## 99 New York 3626 1 -0.352
## 100 New York 3627 1 1.18
## 101 New York 3629 1 0.205
## 102 North Carolina 3708 0.805 0.230
## 103 North Carolina 3711 1.00 0.327
## 104 North Carolina 3713 1 0.389
## 105 Ohio 3901 0.693 0.239
## 106 Ohio 3902 1 5.58
## 107 Ohio 3905 1 -0.112
## 108 Ohio 3906 0.711 0.549
## 109 Ohio 3912 1 0.278
## 110 Ohio 3913 1 0.276
## 111 Ohio 3915 1 -5.99
## 112 Ohio 3916 1 -0.510
## 113 Ohio 3918 1 -1.19
## 114 Oklahoma 4002 1 0.419
## 115 Oklahoma 4005 0.0847 0.0229
## 116 Oregon 4101 1 0.500
## 117 Oregon 4105 0.173 0.0263
## 118 Pennsylvania 4203 1 0.00722
## 119 Pennsylvania 4204 1 -0.0984
## 120 Pennsylvania 4206 1 -1.30
## 121 Pennsylvania 4207 1 -47.9
## 122 Pennsylvania 4208 0.752 -0.0895
## 123 Pennsylvania 4210 0.758 0.447
## 124 Pennsylvania 4211 0.997 0.677
## 125 Pennsylvania 4212 0.0341 -0.0598
## 126 Pennsylvania 4216 0.00486 0.0105
## 127 Rhode Island 4401 1 -0.119
## 128 Rhode Island 4402 1 0.0767
## 129 South Carolina 4505 0.538 -0.711
## 130 Tennessee 4703 1 5.71
## 131 Tennessee 4704 0.560 -0.109
## 132 Tennessee 4709 0.335 0.0153
## 133 Texas 4815 1 0.248
## 134 Texas 4816 1 -1.65
## 135 Texas 4817 1 -5.48
## 136 Texas 4823 0.182 0.190
## 137 Texas 4827 0.907 0.324
## 138 Utah 4902 0.633 0.220
## 139 Utah 4904 0.136 0.187
## 140 Virginia 5102 0.303 -0.351
## 141 Virginia 5105 0.534 0.367
## 142 Virginia 5107 0.387 0.0606
## 143 Virginia 5109 1 -1.03
## 144 Virginia 5110 0.000441 -0.00541
## 145 Virginia 5111 1 0.119
## 146 Washington 5305 0.850 0.214
## 147 Washington 5308 0.973 0.163
## 148 West Virginia 5402 0.974 0.127
## 149 West Virginia 5403 0.639 -0.340
## 150 Wisconsin 5503 1 0.202
## 151 Wisconsin 5507 1 0.0386
## 152 Wisconsin 5508 0.0559 0.327To better understand and visualize these 152 different linear regression models, I created graphs displaying the distributions of the coefficients and r-square values.
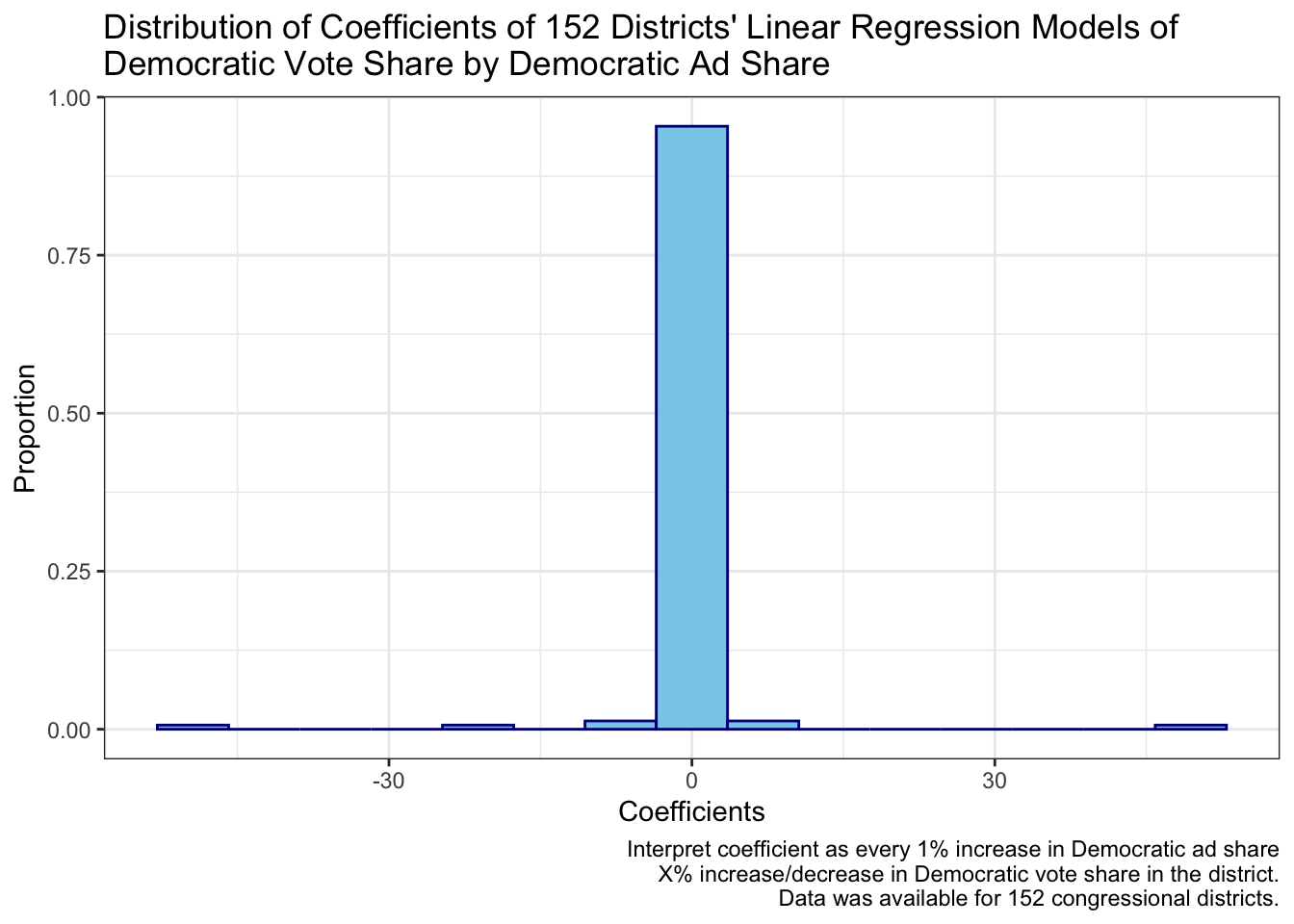
This graph is the distribution of the coefficients of 152 congressional districts from 2006-2018. Almost all of the coefficients fell in the middle “0” range. However, this graph is a bit misleading because the distribution is so widespread that it simplifies the middle of the distribution. Thus, I “zoom” into the middle of the graph to better see the distribution.
## Warning: Removed 10 rows containing non-finite values (stat_bin).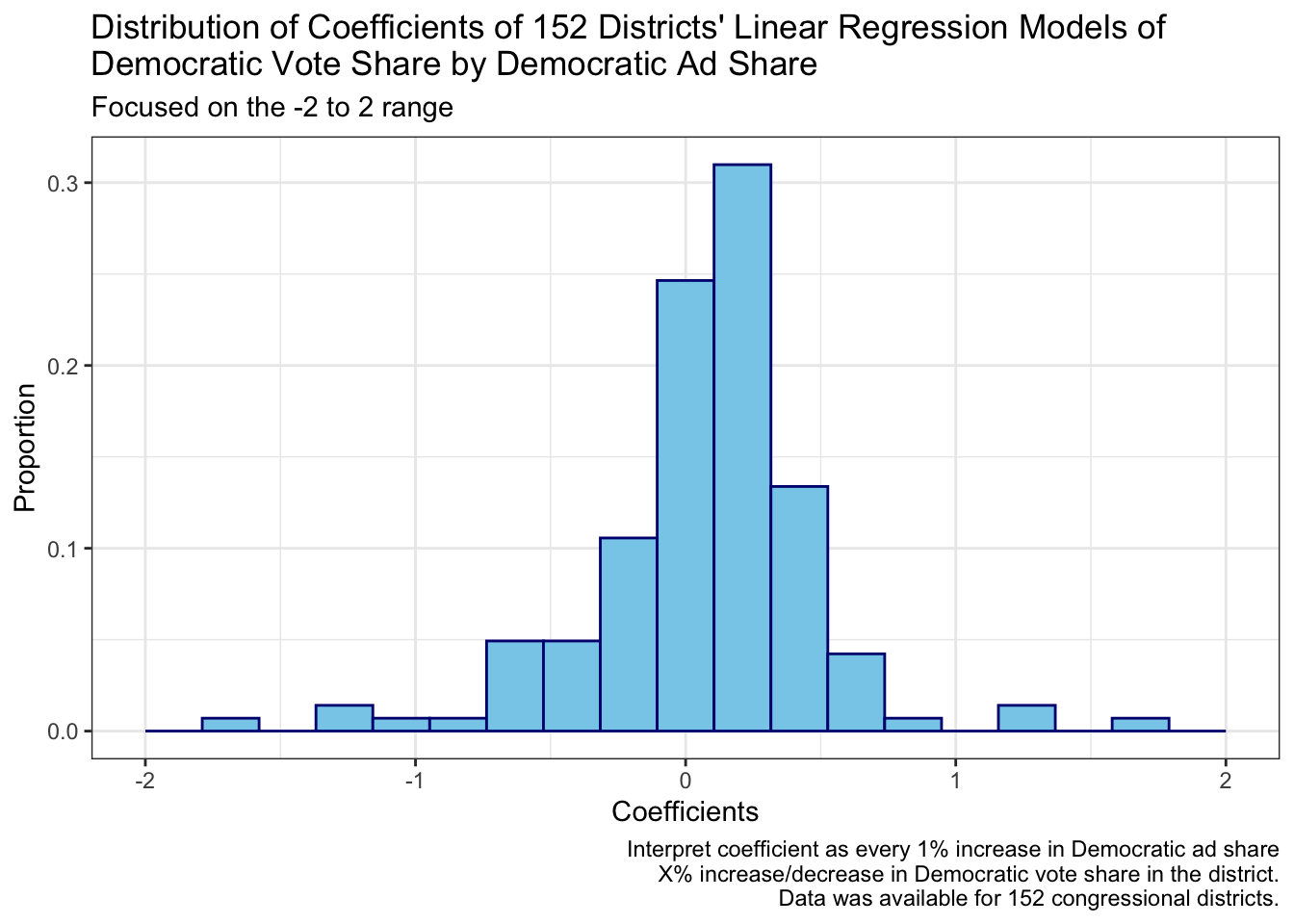
This is the same graph as above but zoomed into the -2 to 2 range. As expected, this “zoom in” has allowed for more nuance in the distribution. Although the distribution is still roughly normally shaped, there is slightly a greater concentration in the positive coefficient zone (>0). This perhaps indicates that there are more districts where there is a positive relationship between Democratic ad share and Democratic vote share than the opposite. In other words, the greater the Democratic ad share, the greater the Democratic vote share.
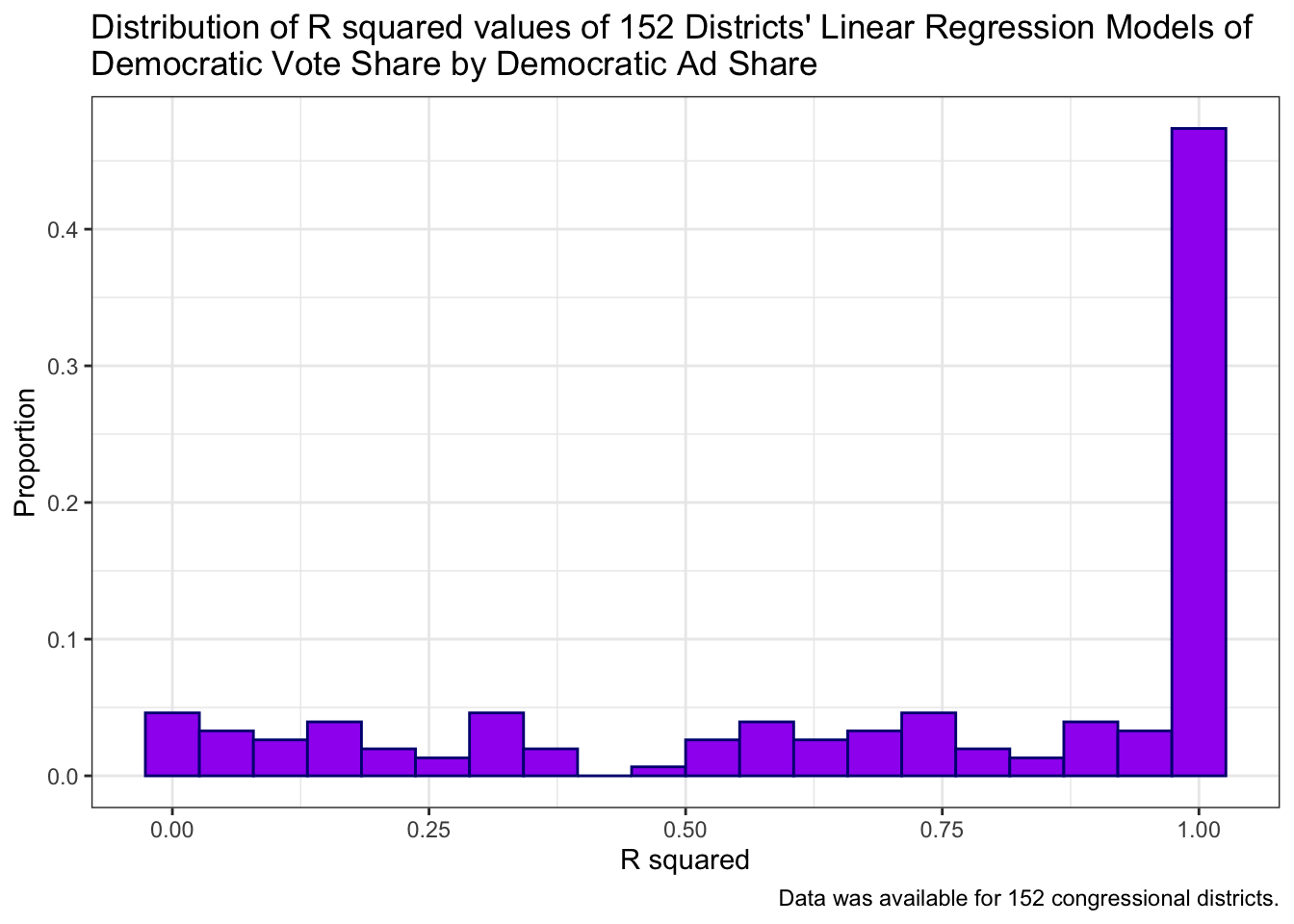
This graph is the distribution of the r-squared values of 152 congressional districts from 2006-2018. Almost 50% of the models have r-squared values of 1, which at first glance is exciting, especially considering that I have had models with negative adjusted r-squared values, but I will talk more about this in my limitations section.
Pennsylvania’s 10th Congressional District
I was not able to run predictions for all 152 congressional districts like I did with the models, so I focused on Pennsylvania’s 10th Congressional District as an example. The current district is located in [south-central region of the state]“https://en.wikipedia.org/wiki/Pennsylvania%27s_10th_congressional_district”, but this is after it was redrawn in 2018. Prior to 2019, the district was located in the northeastern part of the state. This issue of gerrymandering is further explored in my limitations section. Since 2010, the seat, in its many different forms, has been held by a Republican, but prior to 2010 it has been held by a Democrat. The elections in this district are a bit varied with close elections like in 2006 where the Democratic candidate won with 52.90% of the vote or blow out elections like in 2016 where the Republican incumbent won with 70.2% of the vote.
Besides the interesting nature of its election history, I picked PA-10 because the Wesleyan Media Project had data on it for every election between 2006-2018 except 2008.
I ran a linear regression model for Democratic vote share in PA-10 based on Democratic ad share and nation-wide generic ballot polling for the Democrats.
##
## Pennsylvania's 10th Congressional District
## ===================================================
## Dependent variable:
## ---------------------------
## Democratic Vote Share (%)
## ---------------------------------------------------
## Democratic Ad Share (%) 0.352**
## (0.069)
##
## Generic Ballot Polling 1.440*
## (0.439)
##
## Constant -39.773
## (19.346)
##
## ---------------------------------------------------
## Observations 5
## R2 0.967
## Adjusted R2 0.935
## Residual Std. Error 2.601 (df = 2)
## F Statistic 29.664** (df = 2; 2)
## ===================================================
## Note: *p<0.1; **p<0.05; ***p<0.01From this model, we see that for every 1% increase in Democratic ad share, we expect a 0.352% increase in Democratic vote share in PA-10. Similarly, for every 1% increase in the nation-wide generic ballot polling for the Democrats, we expect a 1.440% increase in Democratic vote share in PA-10. The coefficient for Democratic ad share is statistically significant at p=0.05, while the coefficient for generic ballot is statistically significant at p=0.1. Furthermore, the adjusted r-squared value is an astonishing 0.935. However, we must also account for the fact that there are only 5 observations in this model, thus the adjusted r-squared value is not perfect.
###What is the Democratic vote share prediction for Pennsylvania’s 10th district in 2022? Because the data from the Wesleyan Media Project does not have data for 2020 nor 2022, I had to use the 2018 Democratic ad share as a stand-in for 2022. This was 58.67%. In addition, I pulled October 14’s generic ballot polling for Democrats from FiveThirtyEight as the generic ballot polling for 2022. This was 45.8%.
Using the linear regression model from above and this data for 2022, I predict that the Democratic vote share for Pennsylvania’s 10th district in 2022 will be 46.84%.
Limitations
The first limitation with my 152 district models is that the distribution of r-squared values was overwhelmingly 1. This is a bit suspicious and I am in the midst of trying to figure out what happened. I did filter out all districts that only had one row (which would then result in a r-squared value of 1). The second limitation I faced was with my model for PA-10. This district went through multiple rounds of gerrymandering that makes it hard for me to predict for the current district. This raises a potential difficulty I will face if I want to continue doing district-level modeling and predicting. The third limitation is that the Wesleyan Media Project only had data up until 2018 so I had to use the 2018 data as a stand-in for 2022, but we know from earlier that this 2022 election cycle is on-track to become the most expensive, so the Democratic ad share percentage might be different. The fourth limitation is that this data only looks at TV advertisements. It would be interesting to look at if and how online political advertising affects voter behavior.
Conclusion
This week, I explored at the district-level but faced many problems. Thus, I will consider if I want to continue doing district-level predictions in the future. Nonetheless, it was a good exercise.
Data: House Vote (given by class) Wesleyan Media Project (2006-2018) (given by class) House Generic Ballot Polls 1948-2020 (given by class)